Research:Self Correcting Quantum Computers
Our confidence that the quest to build a large scale robust quantum computer is not a wild goose chase arises from the theory of fault-tolerant quantum computation. This theory tells us that if noise on a quantum system is weak enough, and our control over the quantum system is precise enough, then robust large scale quantum computation is possible with only a small (polylogarithmic) blow up in the size of the quantum circuits needed to achieve this robustness. In spite of this theory, however, there are considerable difficulties to the construction of physical systems which enact fault-tolerant quantum computation. In particular the device complexity of most fault-tolerant quantum error correcting routines is quite severe. Is there a better way to build a robust quantum computer than by using the complex and costly currently known fault-tolerant constructions?
We are persuing one possible alternative towards the standard method for constructing fault-tolerant quantum computers. The basic idea is motivated by examining why classical computers are able to perform fault-tolerant quantum computation. In particular we are investigating physical systems which have custom designed Hamiltonians such that the energy eigenvectors of these Hamiltonians are quantum error correcting codes and such that there is a free energy barrier preventing errors from ocuring on this information. Such systems would "self-correct" in much the same way that spin domains on classical hard drives self-correct errors when kept below a critical temperature. For a detailed explanation of what this project is about, scroll down below the references.
References
- D. Bacon, Stability of Quantum Concatenated Code Hamiltonians, Phys. Rev. A, 78, 042324 (2008)
- D. Bacon, Operator Quantum Error-correcting Subsystems for Self-correcting Quantum Memories. Physical Review A, 73, 012340 (2006)
- D. Bacon, K.R. Brown, and K.B. Whaley, Coherence-Preserving Quantum Bits. Physical Review Letters, 87, 247902-1-247902-4 (2001)
- D. Bacon, Decoherence, Control, and Symmetry in Quantum Computers. Ph.D. thesis, University of California, Berkeley, CA (2001)
Contents
Quantum Computing, a Hairbrained Idea?
Quantum computing, at first sight, sounds like a hairbrained idea with absolutely no possible possibility of actually working in the real world. The reasons for this are plentiful, at least when you first start learning about quantum computers. Quantum states are described by a continuum of values. Uh, oh, that sounds a lot like analog computing, which, if you really allow infinite precision, you will get you nearly unlimited power. But in the real world analog computers do not gain this power exactly because real world experiments can only access finite precision. Quantum gates are described by unitary matrices. Again these have a continuum of values. Quantum states "collapse" when you look at them. How do you quantum compute if simply looking at your computer destroys its computation?
Now each of these objections is an objection which was raised back in the days of lore, when Richard Feynman and others first proposed the idea of a quantum computer, and when most physicists and computer scientists didn't even know enough about quantum computing to shun it without learning it. But these objections, when you dig down and analyze them aren't much different from those of a different type of machine, a classical probabilistic machine.
Setup: a Common Category Error
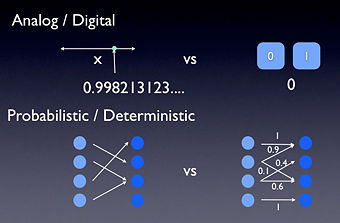
Let me explain. First of all it is useful to define a few things. In particular it is useful to define digital and analog, or at least to define what I mean by these words. To me a digital system is a system whose configurations are a finite set. In other words a digital system has configurations which you might label as zero, one, two, etc, up to some final number. Now of course, most digital systems are abstractions. For example the digital information represented by voltages in your computer is digital in the sense that you define a certain voltage range to be a zero and another range to be one. Thus even though the underlying system may not be digital, from the perspective of how you use the computer, being digital is a good approximation. Analog systems, as opposed to digital systems, are the ones whose configurations aren't drawn from a finite set. Thus, for example, in classical physics, an analog system might be the location of a bug on a line segment. To properly describe where the bug is we need to use the infinite set of real numbers.
Okay, so digital and analog are words which we use to describe the configurations of a physical system (physicists would call these degrees of freedom.) But often a physical system, while it may be digital or analog, also has uncertainty associated with it. Thus it is useful to also make a distinction between systems which are deterministic and those which are probabilistic. Now technically these two ideas really refer to how a systems configurations change with time. But they also influence how we describe the system at a given time. A deterministic system is one in which the configuration at some time is completely determined by the configuration at some previous time. A probabilistic system is one in which the configurations change and, either because we are ignorant of information or for some more fundamental reason, these changes are not known with certainty. For systems which evolve deterministically, we can write down that we know the state of the system. For systems which evolve probabilistically, we aren't allowed to describe our system in such precise terms, but must associate probabilities to be in particular configurations.
Now why am I being so pedantic in describing these words? Well because first of all there is often a confusion between analog systems and probabilistic systems. The first refers to degrees of freedom or configurations. The second refers to how a system changes in time, or what we can predict about it once we make a measurement on it. This category error has caused great confusion.
So what does this have to do with quantum computers? Well it turns out that the set made of deterministic and probabilistic really has another member, and this member is quantum. Quantum theory is the language which describes how systems evolve in time in our universe. Thus we are led, in our most fundamental physical theories, to descriptions of systems which are quantum mechanical. These systems can be analog or digital, but they are described in a quantum fashion. In particular, for probabilistic systems we described our configuration by a set of positive real numbers which sum to unity, while for quantum systems these numbers are replaced by amplitudes, complex numbers whose absolute value squared sum to unity. A quantum system is as simple as that: a system whose description is given by amplitudes and not probabilities.
Why Is Classical Computation Possible?
Classical computers are both digital and deterministic. But if you go and take a microscope to your classical computer what you will see isn't anything like these two categories. For example, if you go and look at the electrons in your silicon based transistor, not all of the electrons are doing the same things. Even in todays ultra pure system, real systems have defects (are dirty) and the electrons in the system are behaving in all sorts of strange ways. Of course the aggregate effect of all of these electrons bouncing around and doing all sorts of crazy things is, when digitized, deterministic. Thus the transistors in your computer are digital and deterministic in spite of the fact that the systems out of which they are constructed are both analog and probabilistic (or worse analog and quantum!) How is this possible? How is it possible to take probabilistic (read noisy) classical analog systems and turn them into deterministic digital computers? The answer to these questions isn't as obvious at first thought as you might think. The first part of the answer is how to go from analog to digital. This is done, in most physical systems, by applying a discretization to some analog set of configurations. Of course, any such discretization must map some values which are nearby in an analog space to differing digital values. So there are always precision questions in defining digital configurations. But, and here is an important point, it is often possible to take an analog system and keep it out of the regimes of difficulty.
Okay so going from analog to digital seems fairly straightforward. But what about going from probabilistic to deterministic. This problem, of how to take systems which change in time according to probabilistic laws, and turn them into systems which compute deterministically has quite a few answers. If we approach this problem from a simple theoretical perspective, then the answer really comes from the theory of classical error correction, and its further extension to the theory of fault-tolerant classical computation. The former of these is founded in the groundbreaking work of Claude Shannon. What Shannon and others showed was that if a classical system is sent through a probabilistic channel which destroys deterministic information, then repeated use of this channel, along with the ideas of classical error correction, can be used to make this probabilistic channel behave nearly deterministically (where nearly means as close to nearly as you want with a good scaling in the resources used.)
The basic idea of classical error correction is simple. If you are sending information down a line where these information can be distorted, then you can lessen the probability of this distortion by encoding your message redundantly. When such an encoding is performed on information, then after it is sent down the noisy line, a suitable decoding can be performed such that if the noise is not too strong, the probability of correctly transmitting the information is greater than if it was just used without the encoding. So, by using classical error correction, one can turn a channel where information evolves probabilistically into one which behave much less probabilistically. If enough encoding is used, this makes the transmission of information effectively deterministic.
A refinement of the idea of classical error correction is the idea of fault-tolerant computation. This is the study of what happens when you are not just transmitting information down a noisy/probabilistic channel, but also allow all of the components of your computer to fail. Thus for instance, in fault-tolerant computation, things like your logic gates can act probabilistically. Further even things like preparing a classical system in a well defined state can be taken into account in fault-tolerant computation. Von Neumann was one of the first to consider how to build an entire computer out of components which were probabilistic. Von Neumann's theory showed, that in principle, if noise was not too strong, then it is possible to build a fault-tolerant classical computer out of faulty components.
The Physics of Classical Information Storage
Despite the fact that Shannon and von Neumann showed that, a least in theory, a reliable, fault-tolerant computer could be built out of faulty, probabilistic components, if we look at our classical computing devices it is not obvious that these ideas matter much. I mean really, once you see how reliable modern transistors or magnetic media work, it is easy to forget that deep down they are highly analog and probabilistic devices. So this leads one to the question of how to reconcile the observations of Shannon and von Neumann with our everyday computing devices. The answer to this seeming conundrum is that systems like transistors and magnetic media actually enact the ideas of the classical theory of error correction, but they do this via the physics of the devices out of which the computer is built.
Let's examine a concrete example of how this works. This will be a cartoon model but it will capture a lot of why you hard drive is able to robustly store information. Our model is made up of a large number of "spins" which are arranged in a regular lattice. For our purposes, let's just make this a two dimensional lattice. These "spins" are simple binary systems which have two configurations, pointing up or pointing down. Now associate with a configuration of the spins (i.e. an assignment of values of pointing up or pointing down) an energy. This energy is calculated in a straightforward way: for each two neighbors on the lattice, add to the energy a value of +J if the spins are pointing in different directions or subtract from the energy a value of -J if the spins are pointing in the same directions. From this description it is easy to see that the lowest energy configuration of spins is when they all point up or when they all point up, since in this configuration all links in the lattice contribute an energy -J in this configuration. Now for any particular configurations of the spins, we can count the number of spins which are pointing up and the number which are pointing down. This is roughly how "information" can be encoded into a device. If the majority of the spins are pointing up, we call this configuration "0". If a majority of the spins are pointing down, we call this configuration "1".
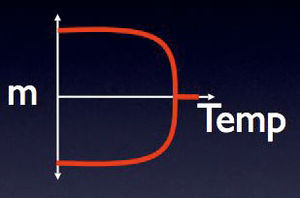
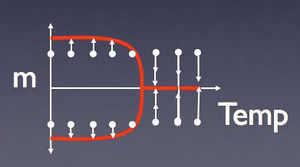
Okay, so how can we view a magnetic media in terms of classical error correction. Well first of all note that we have encoded "0" and "1" by copying their values across a large number of spins. This is what is called a redundancy code in classical error correction. But, now, here is the important point: the system also performs error correction. In particular consider staring the system with all the spins pointing up. If you now flip a single spin, this will cost you some energy because now your spin will be unaligned with the four neighboring spin. Further if you want to flip another spin, this will cost you even more energy. In general one can see that it requires an amount of energy proportional to the perimeter of a domain to flip all of the spins in this domain. Now at a given temperature, the environment of the hard drive is exchanging energy with the system and is constantly fouling up the information of the value of spins. Sometimes energy goes from the environment to the system and the system is driven from one of the two encoded states of all up or all down. Sometimes energy goes the other way from the system to it's environment. This latter process "fixes" the information by driving back towards the encoded state it came from. At a given temperature, the ratio of the rate of these two processes is related to the temperature of the system/envornment. At low enough temperature, if you store information into the all up or all down configuration, then this information will remain there, essentially forever, as the process of cooling beats out the process of heating. At high enough temperature this fails, and the information which you try to store into such a system will be rapidly destroyed. The figure on the right is the way that physicists would talk about these effects. At low temperature, most of the spins are pointing along one of two different directions. As one raises the temperature most of the spins remain pointing mostly up and mostly down, until one nears a critical temperature. At this critical temperature, these two configurations merge into one and information can no longer be reliably store in the equilibrium configurations of this system. Thus we see that one can encode information into the majority vote of these spins, and, at low enough temperature, the rate of errors occurring on the system is dominated by the processes of the errors being fixed. Thus physics does error correction for you in this setup.
Another important property of the model just described is that it is also robust to imperfect manipulations. For example, suppose that you attempt to prepare the system into a mostly up state, but you don't do such a good job and a large (but not majority) number of the spins are accidentally prepared in the down state. Then, the above system will "fix" this problem and will take the system prepared imperfectly to one that is closer to a mostly up state. Similarly if you try to flip the value of the spins, if you don't correctly flip all of them, then the system will naturally relax back to its equilibrium value which will have a higher proportion of spins in the correct distribution. Such a system is "self-correcting" in the sense that the error correction is being done not by an external agent, but instead by the natural dynamics of the system.
So, in this simple example, we have seen that physical systems which are currently used to store classical information actually do embody the ideas of Shannon and error correction: it's just that the physics of these devices enacts these ideas behind the scenes. So, a natural question to ask for quantum computers is whether you can build similar systems for quantum information. Of course, before answering this question you'd better know whether it is possible to mimic the classical ideas of error correction and fault-tolerance for a quantum computer.
Quantum Error Correction
Classical error correction worked by encoding classical information across multiple systems and thus protecting the information better than if it was encoded just locally. Fault-tolerant techniques extend these results to the building of actual robust classical computers. Given that quantum theory seems to be quite different from classical theory, an important question to ask is whether the same can be achieved for information encoded in a quantum manner. The answer to this question, of whether quantum information can be successfully protected even when the quantum system being used is exposed to unwanted evolutions, is one of the great discoveries of quantum computing. In 1995, Peter Shor and Andrew Steane showed that, by using some clever tricks, one could perform quantum error correction on quantum systems and therefore preserve quantum information by suitably encoding the quantum information across multiple independently erred systems. This was a remarkable result, and was the beginning of a series of important discoveries about quantum information which showed how a reliable quantum computer was possible, in spite of the seemingly odd nature of quantum information.
The culmination of research in quantum error correction is usually expressed in terms of a result known as the threshold theorem for fault-tolerant quantum computing. This result states that if a quantum system can be controlled with enough precision, and does not enact with its environment too strongly (both below a threshold) then long quantum computations can be enacted with a cost which scales efficiently with the desired computation being enacted. The threshold theorem essentially states that the model of quantum computing is emphatically not the model of an analog computer, and that, assuming we understand how quantum theory and physics works, a large scale quantum computer is possible. That being said, the conditions for the threshold theorem for quantum computation are severe. While small scale quantum computers of a few qubits have successfully been demonstrated, none of the systems has been easily scaled up to a large scale system needed to test the threshold theorem of quantum computing, nor are all of the quantum computers demonstrated below the threshold values in terms of control of the quantum system.
Quantum Hard Drives in Four Dimensions
Given that the quantum error correction is possible, a natural question to ask is whether, like in classical computers, there exist, or whether we can engineer, quantum systems which robustly store quantum information via the physics of these quantum systems. The first to suggest that this might be a viable path toward constructing a quantum computer was Alexei Kitaev. Kitaev suggested that there were certain physical systems, related to topological field theories, where one could encode quantum information into their ground states, and an energetic gap would protect this quantum information from certain errors. The model Kitaev considered could be made into robust storage devices, but were not, by their physics alone, fault-tolerant. Thus, while enacting a computation, Kitaev's original models were not robust to error. A way around this, however, was found: if instead of using Kitaev's model in the two spatial dimensions originally considered, one looked at these models in four spatial dimensions, then the resulting physical system would be self-correcting and fully fault-tolerant due to the physics of these devices. This model, considered by Dennis, Landahl, Kitaev, and Preskill, was, in essence a recipe for constructing a four dimensional quantum hard drive. However, unfortunately, we do not live in a four dimensional world, so this model is not realistic.
Toward Quantum Hard Drives in Real Systems
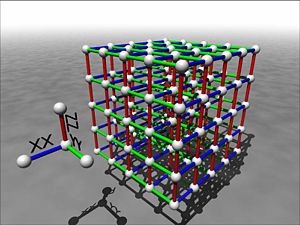
So, given that we know that fault-tolerant quantum computation is possible, under reasonable assumptions, and we know that there exists models of physical systems which can enact these ideas in a natural setting, an important, and vexing problem, is whether we can engineer realistic physical systems which enact these ideas and which don't have bad properties, like only existing in four spatial dimensions. This is the focus of our research on "self-correcting" quantum computers: to develop techniques for building quantum computers whose physical dynamics enacts quantum error correction and which therefore don't need an active quantum error correcting control system. One of our proposed systems, is the three dimensional system seen to the right of this picture. For details on this models see
- D. Bacon, Operator Quantum Error-correcting Subsystems for Self-correcting Quantum Memories. Physical Review A, 73, 012340 (2006)
So, is it possible that building a quantum computer will be done via self-correcting quantum computers? At this point we don't know the answer. We have a few good examples of such self-correcting systems, but none of them, as of yet, are completely reasonable. However a few of them are experimentally accessible and a current project involves really pinning this down and designing the first self-correcting quantum experiment. Look for this page to be updated as progress on this project is made.