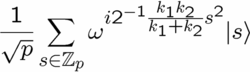Research:The Hidden Subgroup Problem
What new computational tasks can quantum computers perform more efficiently than their classical bretheren? This question is extremely ambitious and is perhaps one which is too big for anyone to ever fully answer. At the same time there is a great need to find new algorithms where quantum computer outperform classical computers. We are interested in finding these new algorithms.
We have focused our initial investigations into new quantum algorithms in the area of nonabelian hidden subgroup problems. An ongoing project focuses on extracting out the crux of why certain nonabelian hidden subgroup problems are efficiently solvable. Efficient quantum algorithms for these problems are important as they could lead to efficient quantum algorithms for graph isomorphism and certain unique-k-shortest vector in a lattice problems.
References
- D. Bacon, Simon's Algorithm, Clebsch-Gordan Sieves, and Hidden Symmetries of Multiple Squares, arXiv:0808.0174
- D. Bacon and T. Decker, The Optimal Single Copy Measurement for the Hidden Subgroup Problem. Physical Review A, 77, 032335 (2008)
- D. Bacon, How a Clebsch-Gordan Transform Helps to Solve the Heisenberg Hidden Subgroup Problem. Quantum Information and Computation, 8, 438-467 (2008)
- D. Bacon, I.L. Chuang, and A.W. Harrow The Quantum Schur Transform: I. Efficient Qudit Circuits. Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, SIAM (Philadelphia, PA, USA) 1235-1244, (2007)
- D. Bacon, I.L. Chuang, and A.W. Harrow, Efficient Quantum Circuits for Schur and Clebsch-Gordan Transforms. Physical Review Letters, 97, 170502 (2006)
- D. Bacon, A.M. Childs, and W. vam Dam, Optimal measurements for the dihedral hidden subgroup problem. Chicago Journal of Theoretical Computer Science, 2, (2006)
- D. Bacon, A.M. Childs, and W. van Dam, From Optimal Measurement to Efficient Quantum Algorithms for the Hidden Subgroup Problem over Semidirect Product Groups. Proceedings of the 46th Annual Symposium on Foundations of Computer Science, IEEE (Los Alamitos, California) 469 (2005)